本篇文章介绍了结构方程模型的两种算法, 一个是基于协方差矩阵的结构方程模型, 简称CB-SEM, 一个是基于最小二乘法的结构方程模型, 简称PLS-SEM, CB-SEM的代表软件是AMOS、MPLUS, PLS-SEM的代表软件是martpls。
本篇文章介绍两种结构方程模型的不同之处, 并在最后附有视频教程。
CB-SEM 基于协方差矩阵的结构方程模型
算法流程
- 计算显变量、测量指标的协方差矩阵、相关矩阵
- 构建SEM模型
- 通过SEM模型反推协方差矩阵、相关矩阵
- 通过算法让模型拟合的协方差矩阵与真实数据的协方差矩阵最像
协方差矩阵
协方差矩阵是一个方阵,其中每个元素表示两个随机变量之间的协方差。协方差矩阵的对角线上的元素是每个随机变量的方差,非对角线上的元素是两个随机变量之间的协方差。¹³⁵
例如,如果有两个随机变量X和Y,它们的协方差矩阵为:
$$\begin{bmatrix} \operatorname{Var}(X) & \operatorname{Cov}(X,Y) \\ \operatorname{Cov}(X,Y) & \operatorname{Var}(Y) \end{bmatrix}$$
结构方程与协方差矩阵的关系
结构方程是什么
我们假定你知道回归分析和因子分析, 那么结构方程模型就很好理解, 结构方程模型就是回归+因子分析.
因子分析就是用多个指标或者问卷题目代表一个因子, 或者说是用多个题目测量一个因子. 回归分析就是分析因子之间的关系.
结构方程模型由两部分组成:测量和结构. 测量部分从概念上理解就是因子分析, 结构部分就可以理解为回归. 但是结构方程与因子分析和回归是完全不同的算法.
结构方程模型(Structural Equation Model,简称SEM)是基于变量的协方差矩阵来分析变量之间关系的一种统计方法,因此也称为协方差结构分析¹。在 SEM 中,协方差矩阵是一个非常重要的概念,因为结构方程的输入数据就是协方差矩阵。协方差矩阵可以用来估计模型参数,从而得到模型的拟合度¹。
我们知道协方差矩阵就是非常好的一个工具, 用于展现变量之间的关系, 变量相关越高协方差就越大. 那么为什么我们还需要做结构方程模型呢? 其实没有什么深奥的道理, 结构方程就是对协方差矩阵的一个简化和提炼, 因为人类无法理解大规模的矩阵, 而结构方程却可以用直观的图来展现变量关系, 对比一下:
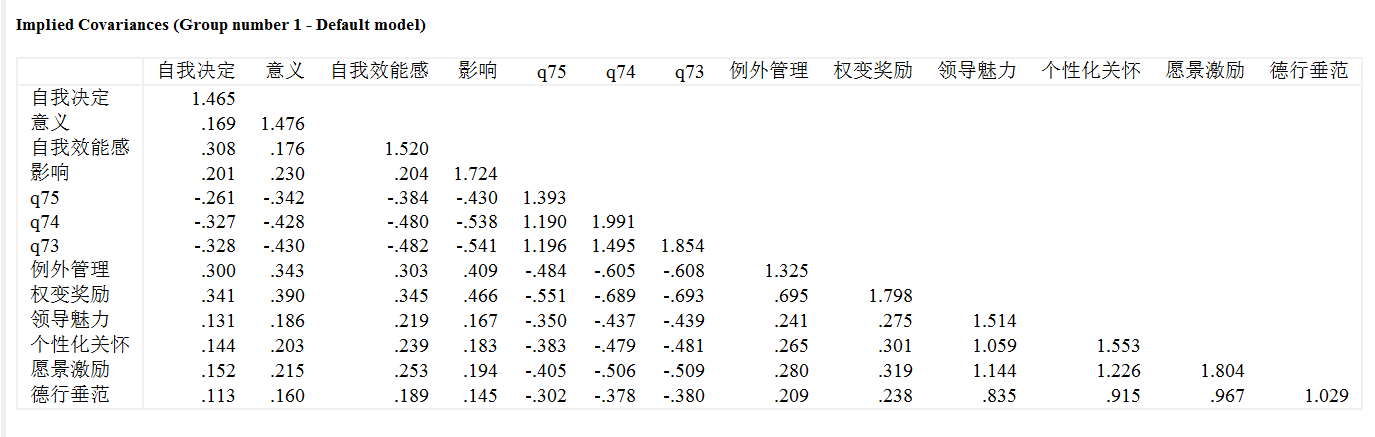
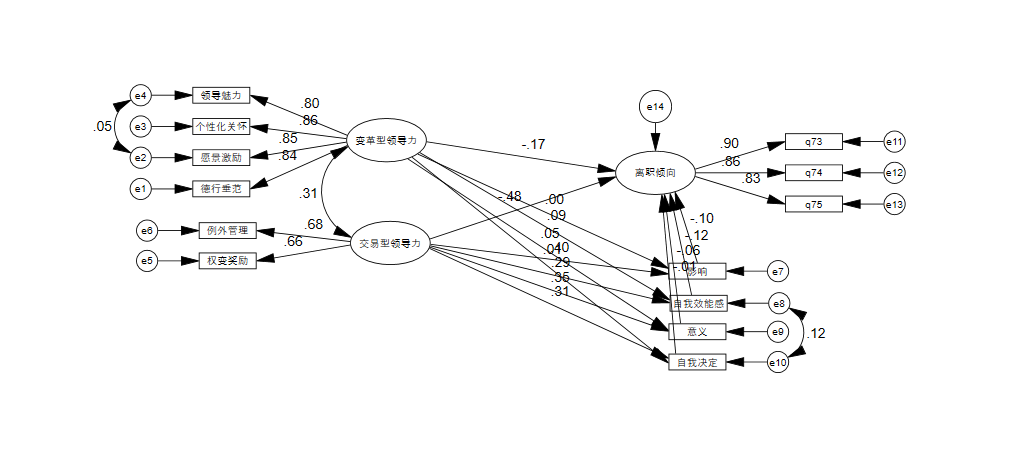
结构方程建模的目的你应该感受到了, 我们从嘈杂的协方差矩阵中首先提炼出来了潜变量(因子), 这个叫做测量模型, 这些潜变量没有出现在协方差当中,
但是为了简化模型, 结构方程用潜变量代表几个测量指标, 用这个潜变量来计算与其他变量之间的关系, 这部分叫做结构模型,
经过模型的提炼, 我们就可以理解变量的关系了, 让人有直观的感受.
拟合指数
对协方差矩阵的提炼得到了结构方程, 结构方程是否能够反映你的协方差矩阵呢? 我们就提出了拟合指数, 说白了就是拟合指数达标意味着你的结构方程模型能够代表你的协方差矩阵. 如果拟合不达标, 意味着你构建的模型无法代表你的协方差矩阵, 即便这个模型多么符合你的预期或者符合理论的预期, 这个模型都是没用的, 因为它不能代表真实的数据.
想要拟合达标是非常简单的, 我们可以让变量之间尽可能多的有连线, 这样拟合出来的模型就是接近完美的:
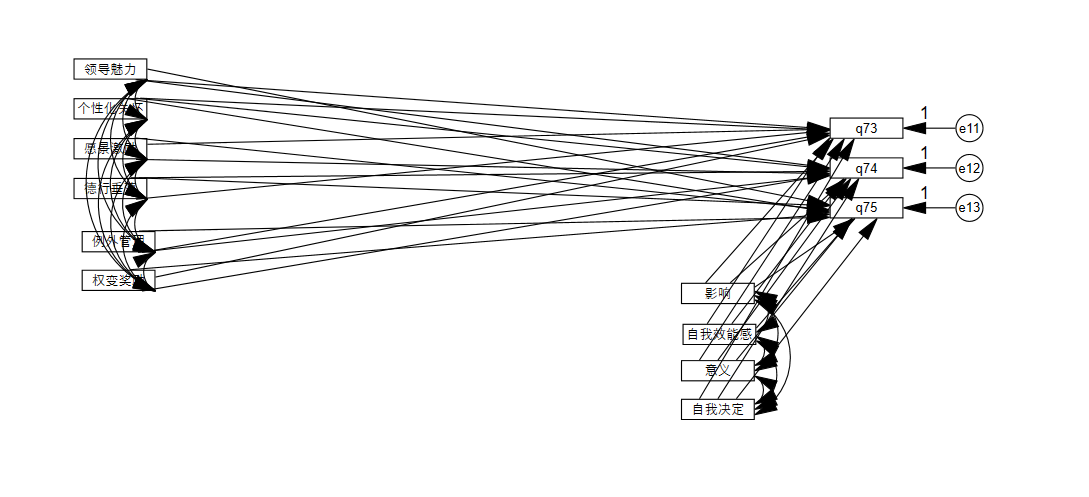
但是正如你所见, 这样的模型是无用的, 无法理解的, 因为它不够简约, 没有理论价值.
所以, 我们结构方程最大的目的就是简化变量关系, 但是关系越简化拟合就会越差, 我们做结构方程就是要用最简约的模型达到最优的拟合, 需要找到一个平衡点.
模型相关矩阵与样本相关矩阵
这是样本相关矩阵:
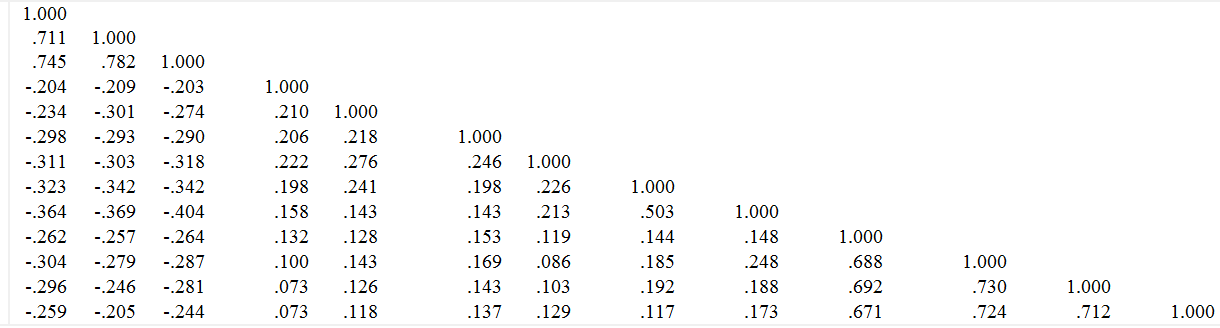
这是模型拟合的相关矩阵:
PLS-SEM 基于最小二乘法的结构方程模型

- Stage 0: 合成潜变量分数, 比如Yj由5个题目, 那么Yj就是5个题目得分的均值
- Stage 1: 循环下面四个步骤直到收敛
- #1: 内部权重, 它指的是变量之间的关系, 当变量之间有直接连线时, 他们之间的内部权重就是这两个变量的协方差
- #2: 内部估计: 经过上一步, 我们已经求得变量的权重, 然后利用权重可以重新计算Yj的估计
- #3: 外部权重: 即潜变量与测量指标之间的权重,因为测量指标分为两种:反映性指标和形成性指标,根据他们的不同定义,形成性指标使用第一个公式,反映性指标使用第二个公式,利用公式可以得到权重w
- #4: 外部估计: 测量指标x是已知的, 上一部计算得到了权重w, 这一步可以使用这两个数据重新计算潜变量Y
- 以上步骤重复进行, 直到收敛, 收敛的意思是参数和变量的变化很小。 收敛后最重要的是得到了潜变量的数据Y
- Stage: 2 and 3: 以上步骤得到了潜变量的数据, 那么所有变量的数据就已经得到, 那么接下来就是求所有的模型参数,包括路径系数、权重等
在2和3阶段使用的就是最小二乘法, 最小二乘法的优化目标就是自变量对因变量的预测误差最小化, 所以使用pls-sem的最大特点是可以对因变量进行预测, 并且得到最优的预测结果, 这是cb-sem所不具有的。
CB-SEM与PLS-SEM的对比

使用PLS而不是CB的原因
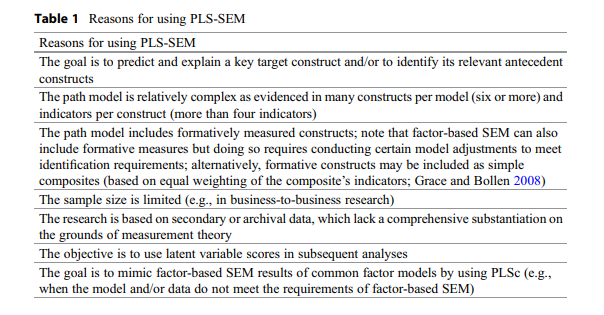
- 目标是变量预测
- 模型太复杂
- 模型中包含形成性指标
- 样本量有限
- 缺乏测量模型
- 需要求得潜变量的分数用于后续分析
- 当数据不满足CB-SEM的要求时,或者模型无法拟合时,不得不采用PLS-SEM
参考文献
- Sarstedt, Marko & Ringle, Christian & Hair, Joseph. (2021). Partial Least Squares Structural Equation Modeling. 10.1007/978-3-319-05542-8_15-2.
注意
统计咨询请加QQ 2726725926, 微信 shujufenxidaizuo, SPSS统计咨询是收费的, 不论什么模型都可以, 只限制于1个研究内.
跟我学统计可以代做分析, 每单几百元不等.
本文由jupyter notebook转换而来, 您可以在这里下载notebook
可以在微博上@mlln-cn向我免费题问
请记住我的网址: mlln.cn 或者 jupyter.cn


